Analysis of Interferometric Wavefront Data¶
In this example, we will see how to use prysm to almost entirely supplant the software that comes with a commerical interferometer to analyze the wavefront of an optic. We begin by importing the relevant classes and setting some aesthetics for matplotlib.
[1]:
from prysm import Interferogram, FringeZernike, sample_files, zernikefit
from matplotlib import pyplot as plt
plt.style.use('bmh')
We point prysm to the file, create a new interferogram, mask it to a circular region 100 mm across, subtract piston, tip/tilt and power, and evalute the PV and RMS wavefront error. We also plot the wavefront.
[2]:
p = sample_files('dat') # sample Zygo .dat file, will be downloaded on demand and saved locally
i = Interferogram.from_zygo_dat(p)
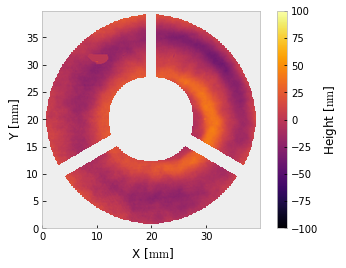
i.crop().mask('circle', 40).crop()
i.remove_piston_tiptilt_power()
print(i.pv, i.rms)
i.plot2d(clim=100, interpolation='bilinear') # +/- 100 nm
plt.grid(False)
83.33634959318245 15.245987053549815
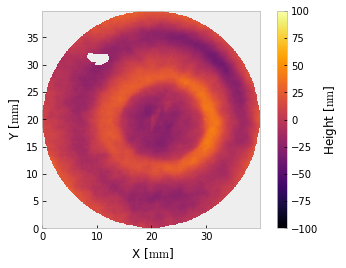
The interferogram is cropped twice – once to enclose the valid data, then again to apply a mask centered on that region. For relatively conventional interferometry, you may want to stop here. If you want to use a different unit, that is easy enough,
[3]:
i.change_z_unit('waves')
1/i.pv, 1/i.rms # print reciprocal -- "one over xxx waves"
[3]:
(7.59332515869843, 41.50600402436136)
There is no need to crop again since the outer bound has not changed. Perhaps you wish to evaluated the RMS within the 1 - 10 mm spatial periods,
[4]:
i.change_z_unit('nm')
i.fill()
i.bandlimited_rms(1,10)
[4]:
4.440527609280636
This value is derived from the PSD, so you must call fill first. Do not worry about the corners of the array containing data - it will be windowed out. If you do this on a part which has a central obscuration or otherwise departs from being a circle or rectangle, the result will be correct.
If you wish to decompose the wavefront into Zernike polynomials, that is easy enough.
[5]:
# do this on data which has not been filled to avoid errors introduced by the fill value.
coefficients = zernikefit(i.phase, terms=36, norm=True, map_='fringe')
fz = FringeZernike(coefficients, dia=i.diameter, z_unit=i.z_unit, norm=True)
print(fz)
rms normalized Fringe Zernike description with:
-1.195 Z1 - Piston
-0.271 Z2 - Tilt Y
+0.484 Z3 - Tilt X
-2.172 Z4 - Defocus
-1.351 Z5 - Primary Astigmatism 0°
+0.324 Z6 - Primary Astigmatism 45°
-0.217 Z7 - Primary Coma Y
-1.655 Z8 - Primary Coma X
-0.241 Z9 - Primary Spherical
+3.036 Z10 - Primary Trefoil Y
-1.244 Z11 - Primary Trefoil X
+1.381 Z12 - Secondary Astigmatism 0°
-0.049 Z13 - Secondary Astigmatism 45°
+2.384 Z14 - Secondary Coma Y
-1.735 Z15 - Secondary Coma X
+6.297 Z16 - Secondary Spherical
+1.349 Z17 - Primary Tetrafoil Y
-0.166 Z18 - Primary Tetrafoil X
-0.842 Z19 - Secondary Trefoil Y
+0.229 Z20 - Secondary Trefoil X
+0.423 Z21 - Tertiary Astigmatism 0°
-0.040 Z22 - Tertiary Astigmatism 45°
-1.042 Z23 - Tertiary Coma Y
+1.362 Z24 - Tertiary Coma X
-2.779 Z25 - Tertiary Spherical
+0.171 Z26 - Primary Pentafoil Y
+0.020 Z27 - Primary Pentafoil X
-0.235 Z28 - Secondary Tetrafoil Y
+0.046 Z29 - Secondary Tetrafoil X
-0.005 Z30 - Tertiary Trefoil Y
-0.005 Z31 - Tertiary Trefoil X
-0.489 Z32 - Quaternary Astigmatism 0°
+0.025 Z33 - Quaternary Astigmatism 45°
+0.106 Z34 - Quaternary Coma Y
-0.192 Z35 - Quaternary Coma X
+0.307 Z36 - Quaternary Spherical
45.208 PV, 9.334 RMS [nm]
This print might be a bit daunting, one may prefer to see the top few terms by magnitude,
[6]:
fz.top_n(5)
[6]:
[(6.296543, 16, 'Secondary Spherical'),
(3.035946, 10, 'Primary Trefoil Y'),
(-2.779492, 25, 'Tertiary Spherical'),
(2.38442, 14, 'Secondary Coma Y'),
(-2.171752, 4, 'Defocus')]
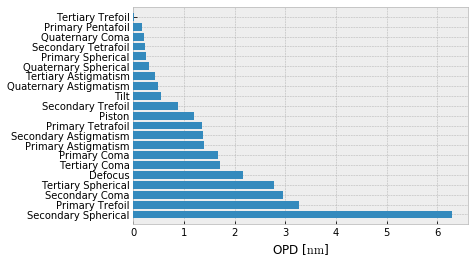
or a barplot of all terms,
[7]:
fz.barplot_magnitudes(orientation='v', sort=True)
[7]:
(<Figure size 432x288 with 1 Axes>,
<matplotlib.axes._subplots.AxesSubplot at 0x7ff213a5a780>)
The sample data has a circular clear aperture, but if it had a central obscuration (such as transmitted wavefront data for a telescope) that would be easy to mask too. Here we will build a composite mask for the data as if it were a telescope with an annual aperture disrupted by a spider:
[8]:
from prysm.geometry import circle, inverted_circle, generate_spider
outer = circle(i.samples_x, radius=1) # radius has units of array semidiameter
inner = inverted_circle(i.samples_x, radius=0.35)
# width has units of arydiam, or pixels if arydiam=None
spider = generate_spider(vanes=3, width=0.5, rotation=90, arydiam=i.diameter, samples=i.samples_x)
mask = outer * inner * spider
i.mask(mask)
i.plot2d(clim=100) # +/- 100 nm
plt.grid(False)